
#Quotient rule calculus low plus#
Simplifying the numerator, you get -3x plus 6 over root x times x plus 2 quantity squared. I think this looks nicer than the one we had before. You do get a root x in the denominator, but that's okay. You'll have 3 times x plus 2, so that's 3x plus 6 minus. The quotient rule is actually the product rule in disguise and is used when differentiating a fraction.The quotient rule states that for two functions, u and. The Quotient Rule The quotient rule says that the derivative of the quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. So multiplying the root x through the numerator, you get a cancellation with this guy. Math Worksheets The quotient rule is used to find the derivative of the division of two functions.

Combine the differentiation rules to find the derivative of a polynomial or rational function. Extend the power rule to functions with negative exponents. Simplifying complex fractions is something that many students are required to do. Use the quotient rule for finding the derivative of a quotient of functions. Actually one thing that you can do about that to get rid of fractions within fractions, these are called complex fractions, is you can multiply the top and bottom of this answer with root x. So this is a little complicated, because we've got a tiny fraction here. To do this, find the lowest number that is divisible by all of your. The chant low-D-high minus high-D-low all over low-low (the D refers to derivative, the low is the denominator and the high is the numerator) is commonly used. So 6 root x times the derivative of x plus 2 which is 1, over the square of what's below. Math Calculus Find the seventh partial sum of 13, 22, 31, 40. There are several ways of remembering the quotient rule. So the derivative of 6 root x is going to be 6 times this. Low d high, x plus 2 times the derivative of this function. X to the -½ is the same as 1 over the square root of x. You get that by thinking of the square root of x as x to the ½. Let me just write this on the side, the derivative. If you use the power rule plus the product rule, you often must find a common denominator to simplify the result. As long as both functions have derivatives. There are two reasons why the quotient rule can be superior to the power rule plus product rule in differentiating a quotient: It preserves common denominators when simplifying the result. Remember the derivative of the square root of x is 1 over 2 root x. The quotient rule is useful when trying to find the derivative of a function that is divided by another function. Here is my low function, here is my high function. So I'm going to use the quotient rule on this. My final answer is 2e to the x over e to the x plus 1 quantity squared. The quotient rule is the formula for taking the derivative of the quotient of two functions. Then minus, minus gives me +1 times e to the x.
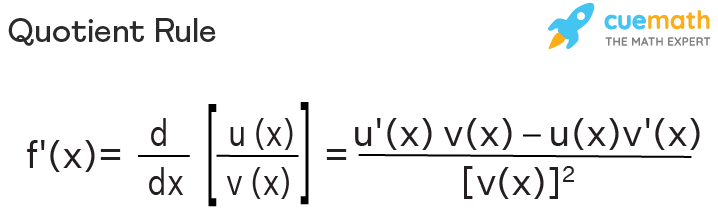
Then I have e to the x times e to the x which is another e to the 2x, so I can see that those are going to cancel. This becomes, I have to the x times e to the x, which is e to the x quantity squared, or e to the 2x plus e to the x minus.

So e to the x, now I'm remembering plus in the denominator, plus 1. It is provable in many ways by using other derivative rules. 1 2 3 Let where both f and g are differentiable and The quotient rule states that the derivative of h(x) is. So e to the x minus 1 times the derivative of this guy which is also e to the x over, the square of what's below. In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. It's going to be low d high e to the x times the derivative of e to the x minus 1, which is e to the x, minus high d low. The quotient rule derivative formula is given as, f (x) u (x)/v (x) v (x) × u (x) - u (x) × v (x)/ v (x) 2. The derivative, dy/dx, is going to be, and I have to use the quotient rule for this guy. (Note that 1/g (x) g (x) (-1). In that equation, because youre adding the two values together, you can move them around without worrying about getting a new value. So the numerator and the denominator are very similar, but this is still an interesting function to look at if you graph it. The quotient rule can be derived from the product rule by writing f (x)/g (x) as f (x) 1/g (x), and using the product, power, and chain rules when differentiating. Here we're asked to differentiate y equals e to the x minus 1 over e to the x plus 1. D d x = d d x ⋅ g ( x ) − f ( x ) ⋅ d d x 2 \dfrac 2 f ′ ( 4 ) g ( 4 ) − f ( 4 ) g ′ ( 4 ) start fraction, f, prime, left parenthesis, 4, right parenthesis, g, left parenthesis, 4, right parenthesis, minus, f, left parenthesis, 4, right parenthesis, g, prime, left parenthesis, 4, right parenthesis, divided by, open bracket, g, left parenthesis, 4, right parenthesis, close bracket, squared, end fraction.


 0 kommentar(er)
0 kommentar(er)
